incorrect resolution smearing

[butler]

Recently, Kathryn Krycka has shown that a) there is a significant difference between NIST's IGOR macros resolution smearing and SasView. b) the SasView result seem very odd. This seems particularly emphasized for some reason when using the power law model.

I will update later with some examples.

[butler]

Updating ticket with information from github PR comments:

@pkienzle chose 2.5 sigma based on the work of Barker & Pedersen (1995). Basically the resolution can be approximated by a truncated Gaussian, but including the long tails will lead to incorrect results. However as @pkienzle points out there is a bit of ambiguity as to whether a ±2.5 or ±3.0 sigma cutoff would be best. The paper states:

The Gaussian method produces fair agreement withh the numerical arc method only by truncation of the Gaussian functions to ± 2.5 sigma. Extending the tails to just ± 3 sigma increase the error intolerably.

and later

Truncating the Gaussian functions at +- 2.5 sigma agian gives the best agreement with the numerical calculation.

although it later says

Here, 2.5 sigma and 3 sigma are chosen only as example truncation limits, with the ideal truncation limits for obtaning good agreement dependent upon the instrumental configuration parameters, and the scattering profile.

John Barker agrees that 2.5 would be best.

@pkienzle also notes:

Limiting the resolution integral to 2.5 sigma on a 1/q⁴ power law model I fit the following slopes:
-4.00 for 20% dq/q
-3.98 for 30% dq/q
-3.92 for 35% dq/q
-1.15 for 40% dq/q
So assuming we keep under 35% dq/q then the fits won't be too badly behaved.

My own testing indicates that the basic obvious problem is fixed when fitting the attached power law type data. However there is an extremely disturbing problem:

If one plots the power law function with default parameters and min max q and then chooses a constant dq% (dq/q), the resulting curve depends sensitively on both the number of points used (default is 50) and much more sensitively on whether choosing those points spaced linearly or logarithmically. To really exacerbate choose a 60% sigmaq/q and 300 points. log spacing will produce a power law of smaller slope but much higher intensity. If one then unclicks the log spacing of points to get linear spacing of points, the curve totally changes to something unrecognizable. This clearly seems very very wrong. The curve should not depend on what points we choose to plot should it? Not sure if the problem is in the smearing algorithm or in the GUI … but suspect it is in sasmodels.

I note that John Barker also has concerns that:

If the power law model follows I(q) = Aq^-m and If you use a "box" shaped resolution function and choose resolution dq = const , (where collimation is dominant), the smeared intensity is

Is(q) = A q^-m + B (dq/q)^2 q^(-m-2)

So for data near the beam stop and m = -4 , the slope on a log-log plot should decrease from -4 down to a limit of -6.
If wavelength smearing is dominant, where dq/q ~ q,

Is(q) = (1 + C (dq/q)^2 ) q^-m

the slope should not change at all, yet you see a large decrease in the slope.

Thus this does seem to fix the obvious problem that was reported but I think some further investigation would be appropriate before merging this PR. It may be that we merge this fix and create a new ticket to investigate the new behavior given that it probably will not be a problem for real systems - though not understanding the underlying cause is worrisome?

[butler]

1m data

[butler]

7m data

[butler]

15m data

[butler]

Lens data

[butler]

data from all 4 configurations spliced into one file

[butler]

ppt showing large deviations (seen as "spikiness" at low q of spliced data

[butler]

While we seem to be closing in on the best way to handle the resolution, the latest change does not entirely fix things. While it now seems to work correctly for reasonable resolutions for extreme cases it does not as shown by the attached report explaining the testing between IGOR and SasView.

The problem occurs for a data set where the resolution cutoff at -2.5 sigma would be beyond zero and thus in negative territory which is never possible. The new code is throwing an error whenever trying to calculate the resolution smeared model. Whether from the truncation or not is unclear but it should be noted that the error is thrown for both data sets. The traceback call is

20:39:29 - INFO : sasmodels.kernelpy:  39: load python model power_law
20:39:29 - ERROR : sas.sasgui.perspectives.fitting.basepage:1620: Traceback (most recent call last):
  File "C:\Users\paperspace\git\sasview\src\sas\sasgui\perspectives\fitting\basepage.py", line 1618, in _update_paramv_on_fit
    self.save_current_state()
  File "C:\Users\paperspace\git\sasview\src\sas\sasgui\perspectives\fitting\basepage.py", line 866, in save_current_state
    self.state.model = self.model.clone()
  File "C:\Users\paperspace\git\sasmodels\sasmodels\sasview_model.py", line 526, in clone
    return deepcopy(self)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 190, in deepcopy
    y = _reconstruct(x, rv, 1, memo)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 334, in _reconstruct
    state = deepcopy(state, memo)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 163, in deepcopy
    y = copier(x, memo)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 256, in _deepcopy_dict
    for key, value in x.iteritems():
RuntimeError: dictionary changed size during iteration 

[butler]

15m data altered for constant 50% sigmaq/q resolution

[butler]

Results of comparison testing between IGOR and SasView?

[pkienzle]

You can use log scaling to specify the resolution tails, setting the upper limit qhigh = q+n*dq to determine the resolution ratio dq_ratio = qhigh/q, and using that to determine the lower limit qlow = q / dq_ratio. This will preserve the slope on the power law. Unlike linear tails, the low and high limits of the log tails are different so power = 1 will now show a shift.

It's up to the SAS theorists to decide if this is an appropriate distortion to the resolution function, and if so, to apply this patch and update the documentation explaining the choice. Alternatively, replace the gaussian distribution with something that better matches instrumental resolution.

Regarding the predicted bend in the theory function at low q, this may not show up for the file Test50pc.ABS. It seems to be using fixed dq/q instead of using fixed dtheta. Note that the second IGOR plot does not show the curve bending up either.

diff --git a/sasmodels/resolution.py b/sasmodels/resolution.py
index d54d84d..e9b6f7d 100644
--- a/sasmodels/resolution.py
+++ b/sasmodels/resolution.py
@@ -188,8 +188,11 @@ def pinhole_resolution(q_calc, q, q_width, nsigma=PINHOLE_N_SIGMA):
     cdf = erf((edges[:, None] - q[None, :]) / (sqrt(2.0)*q_width)[None, :])
     weights = cdf[1:] - cdf[:-1]
     # Limit q range to +/- 2.5 sigma
-    weights[q_calc[:, None] < (q - nsigma*q_width)[None, :]] = 0.
-    weights[q_calc[:, None] > (q + nsigma*q_width)[None, :]] = 0.
+    qhigh = q + nsigma*q_width
+    #qlow = q - nsigma*q_width
+    qlow = q*q/qhigh
+    weights[q_calc[:, None] < qlow[None, :]] = 0.
+    weights[q_calc[:, None] > qhigh[None, :]] = 0.
     weights /= np.sum(weights, axis=0)[None, :]
     return weights

[butler]

Indeed the test file was meant to be constant dq/q for which the slope should in fact not change. The problem is that id DOES .. in this admittedly pathological case. Question I have is why.

The other question is what the python error is coming from.

[pkienzle]

IGOR macros appear to compute using 20-point gaussian quadrature within [q-3dq, q+3dq]. For broad resolution functions, the lower bound is first set to zero (the quadrature points range within [-0.9931, 0.9931] rather than [-1, 1] so the lowest q point evaluated is never actually zero). Strangely, the high q side is not similarly truncated, so the gaussian quadrature points will be in [0, q+3dq], with the center at (q+3dq)/2 rather than q.

Given a constant dq/q, the lowest q point grows like

   ((-0.9931)*(q+3dq) + q+3dq)/2 ~= 0.0086*q for 50% dq/q

This is presumably why the slope is preserved in IGOR, since unlike SasView, higher q points are not all pulling from the same low q cutoff.

Source:

NCNR_SANS_Package_7.12/NCNR_User_Procedures/Common/GaussUtils_v40.ipf:1740
Smear_Model_N_AAO(…)

[pkienzle]

The traceback in the following indicates a threading bug unrelated to resolution. That is, the sasview_model wrapper is being asked to save state in one thread while another thread is updating it with the intermediate calculation values.

This bug will disappear when we restructure the sasview code to return intermediate values as a separate structure rather than temporarily putting them in the structure during calculation then retrieving them with a separate call (perhaps as part of the beta approximation updates).

Replying to butler:

While we seem to be closing in on the best way to handle the resolution, the latest change does not entirely fix things. While it now seems to work correctly for reasonable resolutions for extreme cases it does not as shown by the attached report explaining the testing between IGOR and SasView.

The problem occurs for a data set where the resolution cutoff at -2.5 sigma would be beyond zero and thus in negative territory which is never possible. The new code is throwing an error whenever trying to calculate the resolution smeared model. Whether from the truncation or not is unclear but it should be noted that the error is thrown for both data sets. The traceback call is

20:39:29 - INFO : sasmodels.kernelpy:  39: load python model power_law
20:39:29 - ERROR : sas.sasgui.perspectives.fitting.basepage:1620: Traceback (most recent call last):
  File "C:\Users\paperspace\git\sasview\src\sas\sasgui\perspectives\fitting\basepage.py", line 1618, in _update_paramv_on_fit
    self.save_current_state()
  File "C:\Users\paperspace\git\sasview\src\sas\sasgui\perspectives\fitting\basepage.py", line 866, in save_current_state
    self.state.model = self.model.clone()
  File "C:\Users\paperspace\git\sasmodels\sasmodels\sasview_model.py", line 526, in clone
    return deepcopy(self)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 190, in deepcopy
    y = _reconstruct(x, rv, 1, memo)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 334, in _reconstruct
    state = deepcopy(state, memo)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 163, in deepcopy
    y = copier(x, memo)
  File "C:\ProgramData\Anaconda2\lib\copy.py", line 256, in _deepcopy_dict
    for key, value in x.iteritems():
RuntimeError: dictionary changed size during iteration 

[pkienzle]

Set the q lower bound on the resolution calculation to be the same distance from q as the upper bound on a log scale. This preserves the slope of the power law even for very large values of resolution.

Note that the resolution curve from est50pc.ABS is not very smooth. We need to compute more intermediate points between measured data points to calculate the resolution accurately.

[smk78]

Considered good enough for 4.2, and there are other tickets addressing the deeper issues. Will close the ticket.

[pkienzle]

asymmetric resolution window over [-2.5*dq, 3*dq]

[pkienzle]

Reopening the ticket because monte carlo simulations show that the we are cutting off too much of the resolution window at low q values.

Rather than using the new "logarithmic" window:

q_high = q + 3*dq
q*r = q_high  =>  r = q_high/q
q/r = q_low   =>  q_low = q*q / q_high

instead use an asymmetric window with:

q_low = q - 2.5*dq
q_high = q + 3*dq

The following graph shows a Monte Carlo simulation of the resolution in q at pixels at distance 6, 20 and 60 from the beam center for a generic instrument. The resolution integral will be weighted according to the gaussian (orange line), from q_low to q_high (vertical lines). With the current algorithm, the q_low cutoff for the first graph is 0.0045, which is clearly too aggressive, but it is better behaved for higher q values.

This will still give bad behavior for power law with constant dq/q ≥ 0.4, where q_low will include all I(q) below the current q point. We could protect against this by setting a maximum q_low. I believe Igor is using 0.0086*q (see comment:5). We could set our own arbitrary value such as 0.005*q.

[pkienzle]

Note that resolution was computed with my simple SANS resolution Monte Carlo at:

​https://github.com/scattering/sansresolution

For each detector pixel the idea is to create a population of neutrons at the sample (using a triangular wavelength distribution and angular distribution determined by pinhole aperture), then determine the scattering angle required to for that neutron to reach the given detector pixel. Assuming elastic scattering, we can then compute the distribution of q for that pixel.

It would be useful to cross-check the simulation with McStas or Vitesse. Anyone have an instrument model already defined that can do this?

[pkienzle]

To complete the simulation I added sample scattering to sansresolution/res.py.

For each pixel I set the expected intensity by weighting each scattered neutron that can reach the pixel by the I(q) intensity for the corresponding q. Using this simulated data I'm able to recover reasonable parameters for sphere and fractal models, even with extremely poor resolution (e.g., 40% dL/L). It also works for power law models with more practical resolution. Fitting the simulated data with an asymmetric gaussian returns the power law slope of -4.022 ± 0.005, even though the slope of the simulated data may be as bad as -4.75.

DO NOT FIT DIVERGENT MODELS WITH POOR RESOLUTION. The simulation breaks down for the power law model with extreme resolution since I(q) diverges. In essence, the rare neutrons that scatter at extremely small angles have excessive weight in the simulation leading to erratic results. The resolution calculator also breaks in the same conditions, with an incorrect estimate of I(q).

I do not know how bad our diveregence can get for the power law before our model breaks down. Ideally we would measure the same sample with good and bad resolution to make sure we get the same slope back. We sort of do this already since resolution improves as we move away from the beam stop. If we find that our power law models are still over estimating the counts near the beam stop, then we will again need to revise how we are calculating resolution.

The power law behaviour in the simulation does not seem to appear in real samples. Usually this is because the geometry is chosen to exclude direct line of sight between detector and source aperture. Perhaps the lack of intensity in measured samples could be explained even with almost direct line of sight due to the limited number of neutrons on the sample? Of these, only a small number follow the direct path, but the simulation assumes an unlimited number. Multiple scattering may also apply? If you recast the power law as a probability distribution by introducing an infinitesimal cutoff before q=0, the low q probability will become extremely dominant. With a near infinite probability of scattering, the neutron will scatter at every instant, but with an insignificant change in direction. Occasionally there will be a low probability significant change, followed again by many insignificant changes to the new direction. The result might be that high probability scattering is invisible because the infrequent low probability events are more dramatic.

[GitHub <noreply@…>]

In b77f3ff48ab0e11cd5ed0dab5be0f70beea0ac60/sasview:

Merge pull request #160 from SasView?/abs_qmean

Use Q_mean from ABS files to match Igor analysis

closes #1102

[butler]

Ooops that PR was only related to 1102 but does not close it (there is another PR awaiting review that would close it. Am thus manually re-opening this ticket for now.

[butler]

Replying to pkienzle:

I am confused by these graphs. Why is the centroid of the MC neutrons hitting the pixel far from teh beamstop offset from the Gaussian centroid calculation while it is not for the pixel near the detector.

I would have naively expected the opposite. In fact the Q_mean implemented in IGOR I think adjusts only those points near the detector?

Reopening the ticket because monte carlo simulations show that the we are cutting off too much of the resolution window at low q values.

[richardh]

I'm confused too, how is the orange Gaussian being generated? Is there some plotting issue with the blue histograms (should the orange line ideally go through the mid points of the blue histogram bins? - or their left side? - or their right side?)

Sasview has to assume that whatever data is supplied has the correct Qmean so we know where the centre of the resolution Gaussian is, elsewise we have to start "correcting" the input Q values.  [This can get very messy for tof SANS where the resolution function gets assymmetric to the right hand side at higher Q when short wavelengths are included, especially on a long pulse source like ESS.]

Replying to pkienzle:

I am confused by these graphs. Why is the centroid of the MC neutrons hitting the pixel far from teh beamstop offset from the Gaussian centroid calculation while it is not for the pixel near the detector.
I would have naively expected the opposite. In fact the Q_mean implemented in IGOR I think adjusts only those points near the detector?

Reopening the ticket because monte carlo simulations show that the we are cutting off too much of the resolution window at low q values.

[GitHub <noreply@…>]

In 0d87e79dccfe84c7832491c49c3478f9f1633759/sasmodels:

Merge pull request #74 from SasView?/ticket-1104-resolution

Ticket 1102: use asymmetric integration window for resolution, (-2.5,+3.0) sigma

This looks clearly better than the “log basis” currently implemented. However we will want to revisit this. Further notes added to ticket #1102. Merging this for 4.2.0

addresses #1102.

[butler]

Qmin Cuttoff at low Q

[butler]

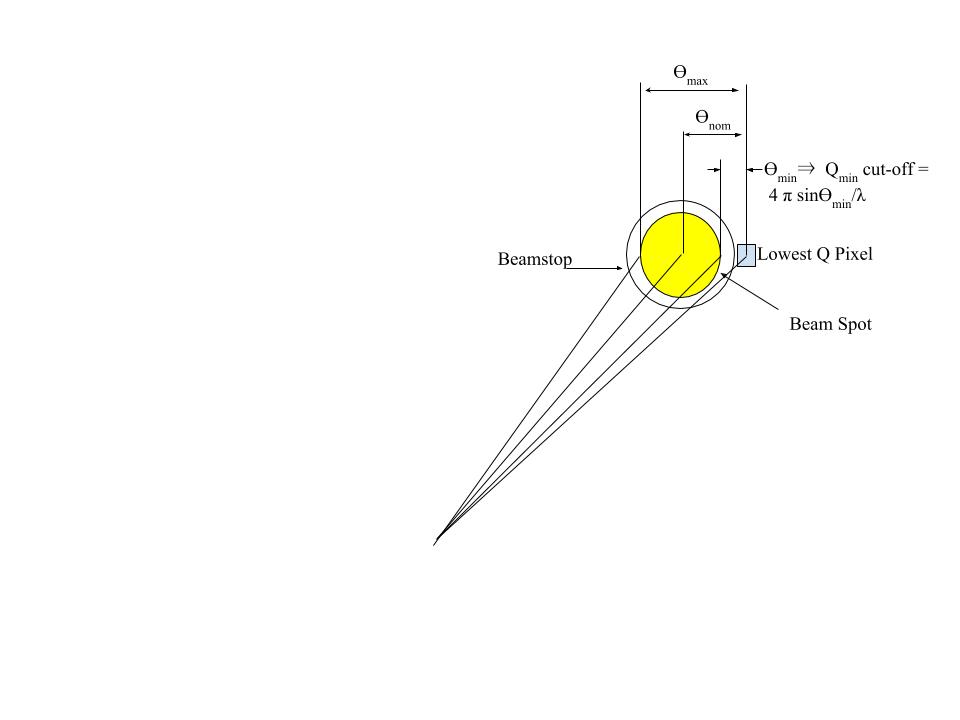
The asymmetric integration window performs better than the previous "log basis" window for broad resolution at low Q. I suspect we will however want to revisit this at some point. There is probably a reason that Steve Kline and John Barker use a Fractional cutoff in the IGOR implementation. The exact value is a bit arbitrary but something of order Qcutoff = 0.8 Qnom is probably good (0.86 is used by John and Steve in IGOR but they also adjust for the skewness of Q close to the detector) for points whose resolution goes over zero? Indeed Qmin is given as in the rough sketch attached and as described in Roger Pynn’ SANS lecture in the 2004 NIST summer school

​https://www.ncnr.nist.gov/summerschool/ss14/pdf/Lecture_5_SANS.pdf

as well as in chapter 15 of Boualem’s SANS toolbox.

​https://www.ncnr.nist.gov/staff/hammouda/distance_learning/chapter_15.pdf

NOTE: Richard Heenan’s point of larger skewness at hight Q is also going to become an issue at some point and we may need to think about what input is needed for that. At the end the data file needs to contain the correct information but SasView also needs to know how to handle said information. NXcanSAS does provide options.

[pkienzle]

The orange line is a Gaussian with mean and std estimated from the Q values for neutrons that can reach the detector pixel evaluated at the bin edges.

The Q values are computed by taking the 2-theta angle between the line-of-sight pixel on the detector for an unscattered neutron and the pixel which is being analyzed. Both line-of-sight and scattered pixel include a gravity correction, but it should be the same for both in this case since I'm looking at pixels along the x-axis.

In terms of nominal vs. actual q, I'm seeing a consistent increase of 0.003 for 4m@6A on NG7, which becomes insignificant as q gets larger. This is mostly due to wavelength, since the average of 1/wavelength is greater than 1/wavelength when the wavelength distribution is symmetric:

pixel j=0
src-ap:5.1cm samp-ap:0.9cm src-dist:7.0m det-dist:4.0m L:6.0A pixel:6,0 (5X5 mm^2)
  nominal 1/lambda: 0.1667  actual 1/lambda: 0.1673 +/- 0.0100 (1/Ang)
  nominal theta: 0.2149  actual theta: 0.2228 +/- 0.0569 (degrees)
  nominal q: 0.0079  actual q: 0.0082 +/- 0.0021 (1/Ang)
pixel j=0
src-ap:5.1cm samp-ap:0.9cm src-dist:7.0m det-dist:4.0m L:6.0A pixel:20,0 (5X5 mm^2)
  nominal 1/lambda: 0.1667  actual 1/lambda: 0.1673 +/- 0.0100 (1/Ang)
  nominal theta: 0.7160  actual theta: 0.7186 +/- 0.0578 (degrees)
  nominal q: 0.0262  actual q: 0.0264 +/- 0.0026 (1/Ang)
pixel j=0
src-ap:5.1cm samp-ap:0.9cm src-dist:7.0m det-dist:4.0m L:6.0A pixel:60,0 (5X5 mm^2)
  nominal 1/lambda: 0.1667  actual 1/lambda: 0.1673 +/- 0.0100 (1/Ang)
  nominal theta: 2.1446  actual theta: 2.1453 +/- 0.0576 (degrees)
  nominal q: 0.0784  actual q: 0.0787 +/- 0.0051 (1/Ang)

I have not looked at John B.'s paper in detail, just the conclusion. Since I'm only looking at detector pixels on the x-axis, I know I'm missing the full effect of gravity, which will change the wavelength distribution as you integrate around the ring. I may be missing other effects as well.

Someone could do the simulation in a trusted code such as McStas or !Vitesse, including the integration around the ring. It should be simple enough to create a pinhole SANS machine with no sample in the beam.

Replying to richardh:

I'm confused too, how is the orange Gaussian being generated? Is there some plotting issue with the blue histograms (should the orange line ideally go through the mid points of the blue histogram bins? - or their left side? - or their right side?)

Sasview has to assume that whatever data is supplied has the correct Qmean so we know where the centre of the resolution Gaussian is, elsewise we have to start "correcting" the input Q values.  [This can get very messy for tof SANS where the resolution function gets assymmetric to the right hand side at higher Q when short wavelengths are included, especially on a long pulse source like ESS.]

Replying to pkienzle:

I am confused by these graphs. Why is the centroid of the MC neutrons hitting the pixel far from teh beamstop offset from the Gaussian centroid calculation while it is not for the pixel near the detector.
I would have naively expected the opposite. In fact the Q_mean implemented in IGOR I think adjusts only those points near the detector?

Reopening the ticket because monte carlo simulations show that the we are cutting off too much of the resolution window at low q values.

[pkienzle]

Note that the skewness is coming from 1/wavelength in the expression for Q.

You can simulate this easily enough:

L,dLoL=6,0.15
samples = L + L*dLoL*randn(1000000)
h=hist(1./samples, bins=linspace(0.1,0.3,400), normed=True)
title("1/L for dL/L=%g"%dLoL)

[richardh]

Replying to pkienzle:

The problem with running Mcstas or Vitesse is that they only generate "raw" data, which then has to be fed through a data reduction code to get to Q space. After that estimating Q resolution (e.g. from a series of perfect Bragg peaks) then requires fitting of the reduced data, all of which is very tedious. So as long as your Monte Carlo does actually mimic the effects of data reduction OK, it is actually a nice efficient code.

[It could perhaps be done by numerical integration instead of MC, array of points on 1st aperture, x array on 2nd aperture x fine array across detector pixels. For 1d data, many pixels may contribute to a single Q bin, which contributes some extra smearing over that from a single pixel. ]

Note that resolution was computed with my simple SANS resolution Monte Carlo at:

​https://github.com/scattering/sansresolution

For each detector pixel the idea is to create a population of neutrons at the sample (using a triangular wavelength distribution and angular distribution determined by pinhole aperture), then determine the scattering angle required to for that neutron to reach the given detector pixel. Assuming elastic scattering, we can then compute the distribution of q for that pixel.

It would be useful to cross-check the simulation with McStas or Vitesse. Anyone have an instrument model already defined that can do this?