Opened 9 years ago
Closed 8 years ago
#776 closed enhancement (fixed)
angular dispersity
| Reported by: | dirk | Owned by: | pkienzle |
|---|---|---|---|
| Priority: | critical | Milestone: | SasView 4.2.0 |
| Component: | sasmodels | Keywords: | |
| Cc: | Work Package: | SasModels Redesign |
Description
Regarding angular dispersity, I had some discussions with a user measuring oriented samples and a theorist simulating disorder in orientation. We concluded that something like the following would be useful:
Given the orientation vector along the axis of the shape as described above, define axial dispersity as a perturbation of this axis. In the isotropic case, the dispersity weight w(x) represents the probability that the shape axis will be found at angle x with respect to the orientation direction, in any direction. For anisotropic dispersity there will be a soft axis with larger dispersity and a perpendicular hard axis with smaller dispersity. For non-rotationally symmetric particles, the rotation vector psi is likely aligned with the hard or the soft axis. There will be a separate rotational dispersity associated directly with psi. For rotationally symmetric particles, any orientational anisotropy will depend on the flow field which defined the alignment, which could be in any direction.
Translating this to SasView? is a bit challenging. We could use latitude, longitude and rotation as the names of the orientation parameters. The usual rotation.width will work for rotational dispersity. Unfortunately, neither latitude.width nor longitude.width is directly tied to the hard and soft axes of the orientation dispersity. We could define latitude.width as expected, and define longitude.width as the distance along the great circle perpendicular to longitude from the given latitude. One of these is the hard axis and the other the soft axis, so all we need is another parameter to which rotates the resulting points about the orientation direction. It would be convenient if the definition we chose happened to align with the shear direction relative to the beam in shear flow experiments with the soft axis in the direction of the flow and the hard axis perpendicular to the flow.
The above definitions should work for strongly oriented samples using gaussian dispersion, which is the majority of the cases we are trying to cover.
Particle orientation can be bimodal. For example, in particles with a thick end and thin end, the thick end or the thin end may be oriented with the shear direction (with a preference for one over the the other) but very few particles will be oriented across the shear. For strongly oriented samples, such systems could be handled with the sum of two models with orientations 180 degrees apart.
Weakly oriented systems will not be well described by our existing distributions. If particles can shift as much as 90 degrees, then they are probably isotropic in that direction (including rotation about the axis). None of our distributions will exhibit this sort of behaviour. We may want to set a default maximum on the angular dispersion at 30 degrees or less, with strong warnings in the manual that we don't understand weakly oriented systems, and the simulations may not be meaningful.
It would be useful to check that our definition supports unoriented samples, ideally defining them as a rectangular distribution of width ±90 for latitude and longitude [NOT the gaussian equivalent rectangular width as defined in SasView?!], with whatever corrections are needed for the polar coordinates integration to produce the right answer. This exercise will provide hints regarding how to interpret weakly oriented samples which are not fully isotropic.
The internal implementation of polydispersity will not support the above definition. Currently we send in a set of values to evaluate for each parameter, but the definition about requires a non-linear transformation that depends on the orientation angle. Rather than centering and scaling in the distribution definition, we could send the distribution (x, w(x)) centered at 0, adding the polydispersity to the parameter value each time through the loop rather than replacing it. The distribution truncation code, which allows us to limit parameters to the min-max range will need to take this into account. Setting limits on orientation parameters should not affect the angular distribution, unlike the polydispersity on shape parameters.
We need to be careful about limits on the angles for the orientation. If they are unlimited, DREAM will happily find multiples of 360 that fit equally well. If longitude is limited to [-180, 180] and the optimal value is near 180, then DREAM will not be able to identify the proper uncertainty distribution because it will be limited to 180. In this case, the fit should be redone with limits in the range [0, 360]. There will be strange effects for latitude 90, since 91 degrees is practically equivalent to 89 degrees in the above definition. Not sure how to handle this case.
Attachments (3)
Change History (20)
Changed 9 years ago by pkienzle
comment:1 Changed 9 years ago by pkienzle
The attached figures show the the proposed orientation mesh for theta, phi but not psi. The application which generated them can be run using:
python sasmodels/explore/angular_pd.py
The axis of the sphere represents neutron direction and the points on the surface represent the orientation of the shape axis wrt the sphere. "roll" or "spin" for shapes which are not circularly symmetric are an independent parameter not shown on the graph.
The "flow" only applies to anisotropic distributions where phi width is different from theta width.
The parameterization of the patch is not ideal. I would rather see theta==phi by default with a separate eccentricity parameter to scale phi so that users don't have to use constraints to encode the common case. Square patches are fine for gaussian distributions since the weights become very improbably at the corners. Rectangular distributions work fine for integrating over the entire sphere as "square" patches given a abs(cos(theta)) term. They may not be meaningful for smaller slices.
comment:2 Changed 9 years ago by pkienzle
For normalization by weight, there may be a factor of 4pi required in order for the integral over a rectangular distribution covering the entire sphere to produce the correct result. Not sure how this affects the Gaussian patch, if at all.
comment:3 Changed 9 years ago by pkienzle
Working on ticket776 branch (https://github.com/sasview/sasmodels/tree/ticket776)
Added ORIENT_SYMMETRIC and ORIENT_ASYMMETRIC macros to kernel_header.c.
Be sure that tests are restored before closing ticket.
These shapes have been updated to use the new macros:
barbell
capped_cylinder
core_shell_bicelle
core_shell_cylinder
core_shell_ellipsoid
cylinder
ellipsoid
hollow_cylinder
stacked_disks
bcc_paracrystal
fcc_paracrystal
sc_paracrystal
triaxial_ellipsoid
elliptical_cylinder
core_shell_parallelepiped
parallelepiped
These shapes use orientation internally, but do not expose them to the user:
hollow_rectangular_prism
hollow_rectangular_prism_thin_walls
rectangular_prism
These shapes might also have oriented forms:
lamellar_…
flexible_cylinder
linear_pearls
pearl_necklace
flexible_cylinder_elliptical
pringle
comment:4 Changed 9 years ago by Paul Kienzle <pkienzle@…>
comment:5 Changed 9 years ago by pkienzle
- Milestone changed from sasmodels Next Release +1 to SasView 4.1.0
comment:6 Changed 9 years ago by Paul Kienzle <pkienzle@…>
comment:7 Changed 9 years ago by Paul Kienzle <pkienzle@…>
comment:8 Changed 9 years ago by GitHub <noreply@…>
comment:9 Changed 9 years ago by butler
- Milestone changed from SasView 4.1.0 to SasView 4.2.0
At fortnightly meeting of Dec 20, 2016 agreed to move this to 4.2 as it is unlikely to be completed and tested by end of January.
comment:10 Changed 9 years ago by richardh
See also comments on #836
comment:11 Changed 9 years ago by pkienzle
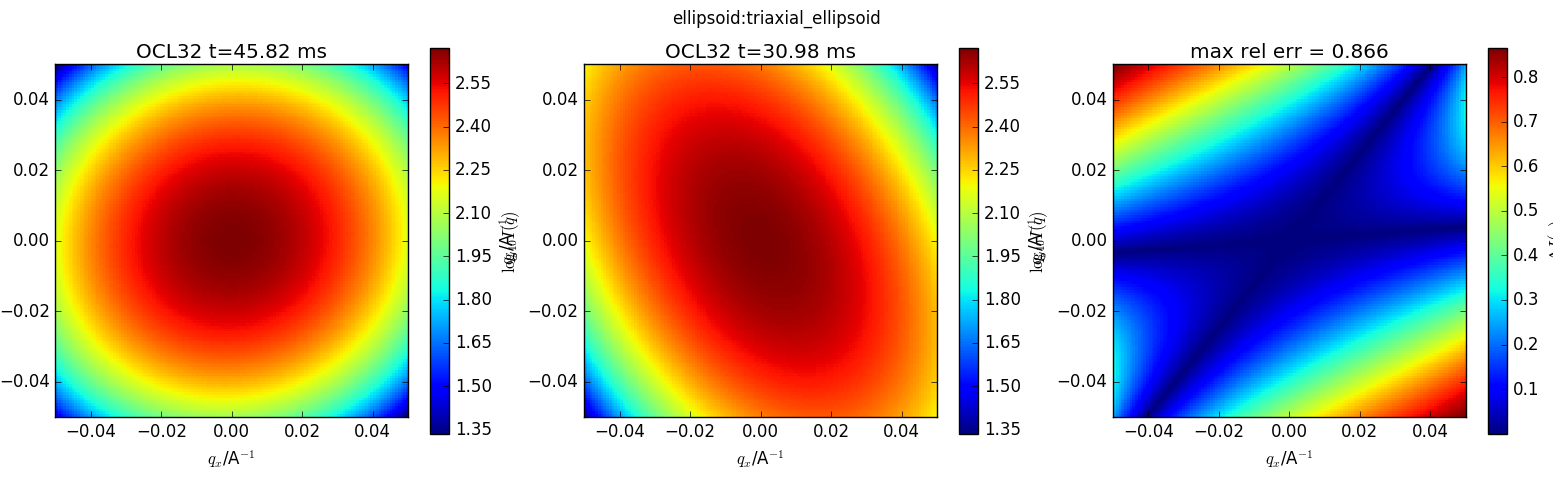
ellipsoid does not match triaxial_ellipsoid with triaxial ellipsoid equatorial major/minor both equal to ellipsoid equatorial
$ sascomp ellipsoid,triaxial_ellipsoid -2d -pars radius_equat_minor=radius_equatorial radius_equat_major=radius_equatorial -mono ==== ellipsoid ===== scale: 1 background: 0 sld: 6 sld_solvent: 1 radius_polar: 50 radius_equatorial: 30 theta: 30 phi: 15 ==== triaxial_ellipsoid ===== scale: 1 background: 0 sld: 6 sld_solvent: 1 radius_equat_minor: 30 radius_equat_major: 30 radius_polar: 50 theta: 30 phi: 15 psi: 5
comment:12 Changed 9 years ago by richardh
Triaxial ellipsoid is one of the asymmetric particles which are still in the old coordinate system.
I think that: cos(theta') = cos(theta)sin(phi) and tan(phi')=tan(theta)/cos(phi)
where the primed angles are the new system, used by the normal ellipsoid.
Thus try ellipsoid with theta 77.04746 phi 30.86748
comment:13 Changed 9 years ago by pkienzle
The ellipsoid with theta 77.04746 phi 30.86748 does match the triaxial ellipsoid.
Note that I had to fix the ellipsoid code first. Last January I introduced a coding error (renaming a parameter sin_alpha instead of cos_alpha, but still calling it with cos_alpha) which later became a calculation error when we changed the coordinate system in October and started calling the ellipsoid kernel with sin_alpha. This effectively swapped the sense of polar/equatorial radius relative to Guinier (1955). It is still correct in the 4.0.1 release, which matches the scattering pattern in 3.1.2.
So how do we compute the new cos_alpha, cos_mu and cos_nu?
comment:14 Changed 9 years ago by richardh
I don't think Dirk has a definitive answer to the questions in the first part of this ticket, perhaps he could comment if he reads this. So I don't think we have a proposal yet for how to handle the psi angle better.
I have not yet attempted to get my head around alpha, mu & nu yet (that's the trouble with only working 2 days a week).
I am concerned that there may be an issue with the psi angle integration in the current code.
Also would be helpful for testing if there was an easy means to specify to integrate over the full range of phi from 0 to 360 deg, this would help with trying to say match elliptical cylinder against normal cylinder.
Pity that ellipsoid is one of the models that has no unit tests, might then have noticed an issue.
comment:15 Changed 9 years ago by pkienzle
You can use a rectangle distribution to integrate about psi.
With psi_pd_type=rectangle and psi_pd_nsigma=1, you can select psi_pd_n points uniformly in (psi-psi_pd, psi+psi_pd) inclusive. For example, to integrate over every degree 0, 1, 2, …, 359, set psi_pd_n=360, psi_pd=179.5 and psi=179.5. You can also set the axis_ratio for the ellipse, and to get the equivalent radius, set "radius_minor=radius/sqrt(axis_ratio)", or equivalently axis_ratio=radius**2/radius_minor**2.
For radius=121, length=400 and axis_ratio=4, this gives:
sascomp -pars -mono -2d psi=179.5 psi_pd=179.5 psi_pd_n=360 psi_pd_nsigma=1 psi_pd_type=rectangle cylinder,elliptical_cylinder axis_ratio=4 radius_minor="radius/sqrt(axis_ratio)" length=400 radius=121
The -pars option prints the parameters. The -mono option forces all other polydisperse parameters in demo to be monodisperse.
The resulting patterns are clearly different. Even without the psi integration, you can set the ellipse to to a circle using radius_minor=radius and axis_ratio=1. Since the asymmetric orientation parameters are not yet set correctly this gives a different result.
We can't use sascomp to compare 1D to 2D since theta integration needs to be weighted by sin(theta). Maybe add a -integrate2d flag to sascomp for testing?
comment:16 Changed 8 years ago by pkienzle
- Priority changed from major to critical
comment:17 Changed 8 years ago by pkienzle
- Resolution set to fixed
- Status changed from new to closed
theta,phi mesh used for current angular dispersity average