Model Functions
- Introduction
- Shapes: SphereModel, CylinderModel, EllipsoidModel, CoreShellModel, CoreShellCylinderModel, EllipticalCylinderModel.
- Shape-Independent: Debye, Lorentz, DAB_Model, Power_Law, Teubner Strey, BEPolyelectrolyte, Number Density Fractal, Guinier, PorodModel.
- Customized Models: A+Bcos(2x)+Csin(2x).
- Structure Factors: HardSphereStructure, SquareWellStructure, HayterMSAStructure, StickyHSStructure.
- References
1. Introduction
The present text documents the modules made available by the DANSE software for SANS.
Readers are also referred to the SANS/DANSE wiki page:
http://danse.us/trac/sans
Users can report a bug at the following URL:
http://danse.us/trac/sans/newticket
2. Shapes (Scattering intensity models)
This software provides form factors for various particle shapes. After giving a mathematical definition of each model, we draw the list of parameters available to the user. Validation plots for each model are also presented. Instructions on how to use the software is available with the source code, available from SVN:
svn co svn://danse.us/sans/releases/sansmodels-x.x
To easily compare to the scattering intensity measured in experiments, we normalize the form factors by the volume of the particle:
![]() (1)
(1)
with
![]() (2)
(2)
where P0(q) is the un-normalized form factor, ρ(r) is the scattering length density at a given point in space and the integration is done over the volume V of the scatterer.
For systems without inter-particle interference, the form
factors we provide can be related to the scattering intensity by the particle
volume fraction:![]() .
.
Our so-called 1D scattering intensity functions provide P(q) for the case where the scatterer is randomly oriented. In that case, the scattering intensity only depends on the length of q. The intensity measured on the plane of the SANS detector will have an azimuthal symmetry around q=0.
Our so-called 2D scattering intensity functions provide P(q, φ) for an oriented system as a function of a q-vector in the plane of the detector. We define the angle φ as the angle between the q vector and the horizontal (x) axis of the plane of the detector.
2.1. SphereModel
This model provides the form factor, P(q), for a monodisperse spherical particle with uniform scattering length density. The form factor is normalized by the particle volume as described below.
2.1.1. Definition
The 1D scattering intensity is calculated in the following way (Guinier, 1955):
 (3)
(3)
where scale is a scale factor, V is the volume of the scatterer, r is the radius of the sphere, bkg is the background level and Δρ (contrast) is the scattering length density difference between the scatterer and the solvent it is in.
The 2D scattering intensity is the same as P(q) above, regardless of the orientation of the q vector.
The returned value is scaled to units of [cm-1] and the parameters of the sphere model are the following:
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0e-6 |
|
Radius |
Å |
60 |
|
Contrast |
Å -2 |
1 |
|
Background |
cm-1 |
0 |
Our model uses the form factor calculations implemented in a c-library provided by the NIST Center for Neutron Research (Kline, 2006).
2.1.2. Validation of the sphere model
Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006). Figure 1 shows a comparison of the output of our model and the output of the NIST software.
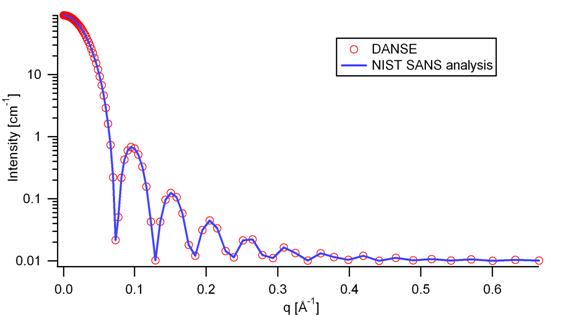
Figure 1: Comparison of the DANSE scattering intensity for a sphere with the output of the NIST SANS analysis software. The parameters were set to: Scale=1.0, Radius=60 Å, Contrast=1e-6 Å -2, and Background=0.01 cm -1.
2.2. CylinderModel
This model provides the form factor for a monodisperse right circular cylinder with uniform scattering length density. The form factor is normalized by the particle volume.
2.2.1. Definition
The output of the 2D scattering intensity function for oriented cylinders is given by (Guinier, 1955):
![]() (4)
(4)
![]() (5)
(5)
where α is the angle between the axis of the cylinder and the q-vector, V is the volume of the cylinder, L is the length of the cylinder, r is the radius of the cylinder, and Δρ (contrast) is the scattering length density difference between the scatterer and the solvent. J1 is the first order Bessel function.
To provide easy access to the orientation of the cylinder, we define the axis of the cylinder using two angles θ and φ. Those angles are defined on Figure 2.

Figure 2: Definition of the angles for oriented cylinders.
The returned value is scaled to units of [cm-1] and the parameters of the cylinder model are the following:
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Radius |
Å |
20.0 |
|
Length |
Å |
400.0 |
|
Contrast |
Å -2 |
3.0e-6 |
|
Background |
cm-1 |
0.0 |
|
Cyl_theta |
Radian |
1.0 |
|
Cyl_phi |
Radian |
1.0 |
The output of the 1D scattering intensity function for randomly oriented cylinders is then given by:
 (6)
(6)
The cyl_theta and cyl_phi parameter are not used for the 1D output. Our implementation of the scattering kernel and the 1D scattering intensity use the c-library from NIST.
2.2.2. Validation of the cylinder model
Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006). Figure 3 shows a comparison of the 1D output of our model and the output of the NIST software.
In general, averaging over a distribution of orientations is done by evaluating the following:
 (7)
(7)
where p(θ,φ) is the probability distribution for the orientation and P0(q,α) is the scattering intensity for the fully oriented system. Since we have no other software to compare the implementation of the intensity for fully oriented cylinders, we can compare the result of averaging our 2D output using a uniform distribution p(θ,φ) = 1.0. Figure 4 shows the result of such a cross-check.

Figure 3: Comparison of the DANSE scattering intensity for a cylinder with the output of the NIST SANS analysis software. The parameters were set to: Scale=1.0, Radius=20 Å, Length=400 Å, Contrast=3e-6 Å -2, and Background=0.01 cm -1.

Figure 4: Comparison of the intensity for uniformly distributed cylinders calculated from our 2D model and the intensity from the NIST SANS analysis software. The parameters used were: Scale=1.0, Radius=20 Å, Length=400 Å, Contrast=3e-6 Å -2, and Background=0.0 cm -1.
2.3. EllipsoidModel
This model provides the form factor for a monodisperse ellipsoid (ellipsoid of revolution) with uniform scattering length density. The form factor is normalized by the particle volume.
2.3.1. Definition
The output of the 2D scattering intensity function for oriented ellipsoids is given by (Feigin, 1987):
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where α is the angle between the axis of the ellipsoid and the q-vector, V is the volume of the ellipsoid, Ra is the radius along the rotation axis of the ellipsoid, Rb is the radius perpendicular to the rotation axis of the ellipsoid and Δρ (contrast) is the scattering length density difference between the scatterer and the solvent.
To provide easy access to the orientation of the ellipsoid, we define the rotation axis of the ellipsoid using two angles θ and φ. Similarly to the case of the cylinder, those angles are defined on Figure 2. For the ellipsoid, θ is the angle between the rotation axis and the z-axis.
The returned value is scaled to units of [cm-1] and the parameters of the ellipsoid model are the following:
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Radius_a (parallel) |
Å |
20.0 |
|
Radius_b (perpendicular) |
Å |
400.0 |
|
Contrast |
Å -2 |
3.0e-6 |
|
Background |
cm-1 |
0.0 |
|
Axis_theta |
Radian |
1.57 |
|
Axis_phi |
Radian |
0.0 |
The output of the 1D scattering intensity function for randomly oriented ellipsoids is then given by equation 6.
The axis_theta and axis_phi parameters are not used for the 1D output. Our implementation of the scattering kernel and the 1D scattering intensity use the c-library from NIST.
2.3.2. Validation of the ellipsoid model
Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006). Figure 5 shows a comparison of the 1D output of our model and the output of the NIST software.
Averaging over a distribution of orientation is done by evaluating equation 7. Since we have no other software to compare the implementation of the intensity for fully oriented ellipsoids, we can compare the result of averaging our 2D output using a uniform distribution p(θ,φ) = 1.0. Figure 6 shows the result of such a cross-check.
The discrepancy above q=0.3 Å -1 is due to the way the form factors are calculated in the c-library provided by NIST. A numerical integration has to be performed to obtain P(q) for randomly oriented particles (equation 6). The NIST software performs that integration with a 76-point Gaussian quadrature rule, which will become imprecise at high q where the amplitude varies quickly as a function of q. The DANSE result shown has been obtained by summing over 501 equidistant points in α. Our result was found to be stable over the range of q shown for a number of points higher than 500.

Figure 5: Comparison of the DANSE scattering intensity for an ellipsoid with the output of the NIST SANS analysis software. The parameters were set to: Scale=1.0, Radius_a=20 Å, Radius_b=400 Å,
Contrast=3e-6 Å -2, and Background=0.01 cm -1.

Figure 6: Comparison of the intensity for uniformly distributed ellipsoids calculated from our 2D model and the intensity from the NIST SANS analysis software. The parameters used were: Scale=1.0, Radius_a=20 Å, Radius_b=400 Å, Contrast=3e-6 Å -2, and Background=0.0 cm -1.
This model provides the form factor, P(q), for a monodisperse spherical particle with a core-shell structure. The form factor is normalized by the particle volume.
2.4.1. Definition
The 1D scattering intensity is calculated in the following way (Guinier, 1955):
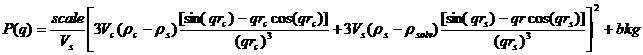 (11)
(11)
where scale is a scale factor, Vs is the volume of the outer shell, Vc is the volume of the core, rs is the radius of the shell, rc is the radius of the core, ρc is the scattering length density of the core, ρs is the scattering length density of the shell, ρsolv is the scattering length density of the solvent, and bkg is the background level.
The 2D scattering intensity is the same as P(q) above, regardless of the orientation of the q vector.
The returned value is scaled to units of [cm-1] and the parameters of the core-shell sphere model are the following:
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Radius |
Å |
60 |
|
Thickness |
Å |
10 |
|
Core_sld |
Å -2 |
1e-6 |
|
Shell_sld |
Å -2 |
2e-6 |
|
Solvent_sld |
Å -2 |
3e-6 |
|
Background |
cm-1 |
0.001 |
Our model uses the form factor calculations implemented in a c-library provided by the NIST Center for Neutron Research (Kline, 2006).
2.4.2. Validation of the core-shell sphere model
Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006). Figure 1 shows a comparison of the output of our model and the output of the NIST software.

Figure 7: Comparison of the DANSE scattering intensity for a core-shell sphere with the output of the NIST SANS analysis software. The parameters were set to: Scale=1.0, Radius=60 Å, Contrast=1e-6 Å -2, and Background=0.001 cm -1.
This model provides the form factor for a monodisperse, circular cylinder with a core-shell scattering length density profile. The form factor is normalized by the particle volume.
2.5.1. Definition
The output of the 2D scattering intensity function for oriented core-shell cylinders is given by (Kline, 2006):
![]() (12)
(12)
 (13)
(13)
where α is the angle between the axis of the cylinder and the q-vector, Vs is the volume of the outer shell, Vc is the volume of the core, L is the length of the core, r is the radius of the core, t is the thickness of the shell, ρc is the scattering length density of the core, ρs is the scattering length density of the shell, ρsolv is the scattering length density of the solvent, and bkg is the background level. The outer radius of the shell is given by r+t and the total length of the outer shell is given by L+2t. J1 is the first order Bessel function.
To provide easy access to the orientation of the core-shell cylinder, we define the axis of the cylinder using two angles θ and φ. Similarly to the case of the cylinder, those angles are defined on Figure 2.
The returned value is scaled to units of [cm-1] and the parameters of the core-shell cylinder model are the following:
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Radius |
Å |
20.0 |
|
Thickness |
Å |
10.0 |
|
Length |
Å |
400.0 |
|
Core_sld |
Å -2 |
1e-6 |
|
Shell_sld |
Å -2 |
4e-6 |
|
Solvent_sld |
Å -2 |
1e-6 |
|
Background |
cm-1 |
0.0 |
|
Axis_theta |
Radian |
1.57 |
|
Axis_phi |
Radian |
0.0 |
The output of the 1D scattering intensity function for randomly oriented cylinders is then given by equation 6.
The axis_theta and axis_phi parameters are not used for the 1D output. Our implementation of the scattering kernel and the 1D scattering intensity use the c-library from NIST.
2.5.2. Validation of the core-shell cylinder model
Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006). Figure 8 shows a comparison of the 1D output of our model and the output of the NIST software.
Averaging over a distribution of orientation is done by evaluating equation 7. Since we have no other software to compare the implementation of the intensity for fully oriented core-shell cylinders, we can compare the result of averaging our 2D output using a uniform distribution p(θ,φ) = 1.0. Figure 9 shows the result of such a cross-check.
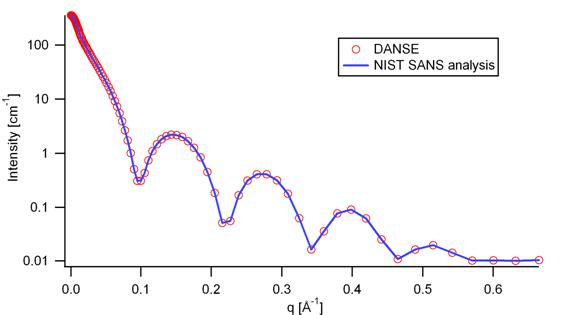
Figure 8: Comparison of the DANSE scattering intensity for a core-shell cylinder with the output of the NIST SANS analysis software. The parameters were set to: Scale=1.0, Radius=20 Å, Thickness=10 Å, Length=400 Å, Core_sld=1e-6 Å -2, Shell_sld=4e-6 Å -2, Solvent_sld=1e-6 Å -2, and Background=0.01 cm -1.

Figure 9: Comparison of the intensity for uniformly distributed core-shell cylinders calculated from our 2D model and the intensity from the NIST SANS analysis software. The parameters used were: Scale=1.0, Radius=20 Å, Thickness=10 Å, Length=400 Å, Core_sld=1e-6 Å -2, Shell_sld=4e-6 Å -2, Solvent_sld=1e-6 Å -2, and Background=0.0 cm -1.
This function calculates the scattering from an oriented elliptical cylinder. The angles theta and phi define the orientation of the axis of the cylinder. The angle psi is defined as the orientation of the major axis of the ellipse with respect to the vector Q. A gaussian poydispersity can be added to any (or all) of the orientation angles, and also for the minor radius and the ratio of the ellipse radii.
The function calculated is:
![]()
with the functions:
 (13)
(13)
and the angle psi is defined as the orientation of the major axis of the ellipse with respect to the vector Q.
The returned value is scaled to units of [cm-1] and the parameters are the following:
|
Parameter name |
Units |
Default value |
|
scale |
None |
1.0 |
|
r_minor |
Å |
20.0 |
|
r_ratio |
Å |
1.5 |
|
length |
Å |
400.0 |
|
contrast |
Å -2 |
3e-6 |
|
cyl_phi |
Å -2 |
0 |
|
cyl_psi |
Å -2 |
0 |
|
cyl_theta |
radian |
1.57 |
|
background |
|
0 |
REFERENCE
L. A. Feigin and D. I. Svergun “Structure Analysis by Small-Angle X-Ray and Neutron Scattering”, Plenum, New York, (1987).
The following are models used for shape-independent SANS analysis.
3.1. Debye (Model)
The Debye model is a form factor for a linear polymer chain. In addition to the radius of gyration, Rg, a scale factor "scale", and a constant background term are included in the calculation.
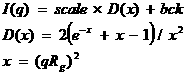
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Rg |
Å |
50.0 |
|
Background |
cm-1 |
0.0 |
Reference: Roe, R.-J., "Methods of X-Ray and Neutron Scattering in Polymer Science", Oxford University Press, New York (2000).
3.2. (Ornstein-Zernicke) Lorentz (Model)
The Ornstein-Zernicke model is defined by:
![]()
The parameter L is referred to as the screening length.
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Length |
Å |
50.0 |
|
Background |
cm-1 |
0.0 |
3.3. DAB(Debye-Anderson-Brumberger)_ Model)
Calculates the scattering from a randomly distributed, two-phase system based on the Debye-Anderson-Brumberger (DAB) model for such systems. The two-phase system is characterized by a single length scale, the correlation length, which is a measure of the average spacing between regions of phase 1 and phase 2. The model also assumes smooth interfaces between the phases and hence exhibits Porod behavior (I ~ Q-4) at large Q (Q*correlation length >> 1).
![]()
The parameter L is referred to as the correlation length.
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
Length |
Å |
50.0 |
|
Background |
cm-1 |
0.0 |
References:
Debye, Anderson, Brumberger, "Scattering by an Inhomogeneous Solid. II. The Correlation Function and its Application", J. Appl. Phys. 28 (6), 679 (1957).
Debye, Bueche, "Scattering by an Inhomogeneous Solid", J. Appl. Phys. 20, 518 (1949).
3.4. Power_Law
This model describes a power law with background.
![]()
Note the minus sign in front of the exponent.
|
Parameter name |
Units |
Default value |
|
Scale |
None |
1.0 |
|
m |
None |
4 |
|
Background |
cm-1 |
0.0 |
This function calculates the scattered intensity of a two-component system using the Teubner-Strey model.
![]()
|
Parameter name |
Units |
Default value |
|
A |
None |
0.1 |
|
C1 |
None |
-30.0 |
|
C2 |
None |
5000.0 |
|
Background |
cm-1 |
0.0 |
References:
Teubner, M; Strey, R. J. Chem. Phys., 87, 3195 (1987).
Schubert, K-V., Strey, R., Kline, S. R. and E. W. Kaler, J. Chem. Phys., 101, 5343 (1994).
3.6. Number Density Fractal (Model)
Calculates the scattering from fractal-like aggregates built from spherical building blocks following the Texiera reference. The value returned is in cm-1.

The scale parameter is the volume fraction of the building blocks, R0 is the radius of the building block, Df is the fractal dimension, ξ is the correlation length, ρsolvent is the scattering length density of the solvent, and ρblock is the scattering length density of the building blocks.
|
Parameter name |
Units |
Default value |
|
Scale |
None |
0.05 |
|
Radius |
Å |
5.0 |
|
Fractal_dim |
None |
2 |
|
Corr_length |
Å |
100.0 |
|
Block_sld |
Å-2 |
2e-6 |
|
Solvent_sld |
Å-2 |
6e-6 |
|
Background |
cm-1 |
0.0 |
References:
J. Teixeira, (1988) J. Appl. Cryst., vol. 21, p781-785
Calculates the structure factor of a polyelectrolyte solution with the RPA expression derived by Borue and Erukhimovich. The value returned is in cm-1.

K is a contrast factor of the polymer, Lb is the Bjerrum length, h is the virial parameter, b is the monomer length, Cs is the concentration of monovalent salt, α is the ionization degree, Ca is the polymer molar concentration, and bck is the incoherent background.
|
Parameter name |
Units |
Default value |
|
K |
Barns = 10-24 cm2 |
10 |
|
Lb |
Å |
7.1 |
|
h |
Å-3 |
12 |
|
b |
Å |
10 |
|
Cs |
Mol/L |
0 |
|
Alpha |
None |
0.05 |
|
Ca |
Mol/L |
0.7 |
|
Background |
cm-1 |
0.0 |
References:
Borue, V. Y., Erukhimovich, I. Y. Macromolecules 21, 3240 (1988).
Joanny, J.-F., Leibler, L. Journal de Physique 51, 545 (1990).
Moussaid, A., Schosseler, F., Munch, J.-P., Candau, S. J. Journal de Physique II France
3, 573 (1993).
Raphaël, E., Joanny, J.-F., Europhysics Letters 11, 179 (1990).
3.8. Guinier (Model)
A Guinier analysis is done by linearizing the data at low q by plotting it as log(I) versus Q2. The Guinier radius Rg can be obtained by fitting the following model:
![]()
|
Parameter name |
Units |
Default value |
|
scale |
cm-1 |
1.0 |
|
Rg |
Å |
60 |
3.9. PorodModel
A Porod analysis is done by linearizing the data at high q by plotting it as log(I) versus log(Q). In the high q region we can fit the following model:
![]()
C is the scale factor and Sv is the specific surface area of the sample and Δρ is the contrast factor.
The background term is added for data analysis.
|
Parameter name |
Units |
Default value |
|
Scale |
Å-4 |
0.1 |
|
Background |
cm-1 |
0 |
These models are defined by users (See SansView tutorial for details).
4.1. A+Bcos(2x)+Csin(2x)
This function, as an example function, calculates intensity = A + Bcos(2Q) + Csin(2Q).
The information in this section is originated from NIST SANS IgorPro package.
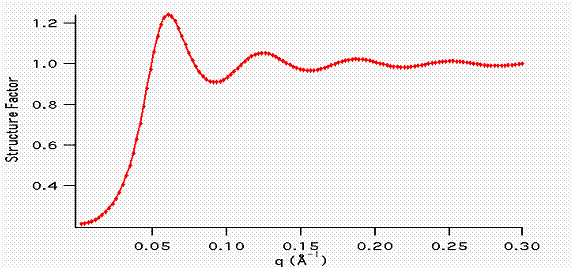
5.1. HardSphere Structure
This calculates the interparticle structure factor for monodisperse spherical particles interacting through hard sphere (excluded volume) interactions. The calculation uses the Percus-Yevick closure where the interparticle potential is:
![]()
where r is the distance from the center of the sphere of a radius R.
|
Parameter name |
Units |
Default value |
|
radius |
Å |
50.0 |
|
volfraction |
|
0.2 |
References:
Percus, J. K.; Yevick, J. Phys. Rev. 110, 1. (1958).
5.2. SquareWell Structure
This calculates the interparticle structure factor for a squar well fluid spherical particles The mean spherical approximation (MSA) closure was used for this calculation, and is not the most appropriate closure for an attractive interparticle potential. This solution has been compared to Monte Carlo simulations for a square well fluid, showing this calculation to be limited in applicability to well depths e < 1.5 kT and volume fractions f < 0.08.
Positive well depths correspond to an attractive potential well. Negative well depths correspond to a potential "shoulder", which may or may not be physically reasonable.
The well width (l) is defined as multiples of the particle diameter (2*R)
The interaction potential is:
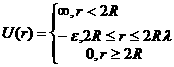
where r is the distance from the center of the sphere of a radius R.
|
Parameter name |
Units |
Default value |
|
radius |
Å |
50.0 |
|
volfraction |
|
0.2 |
|
welldepth |
kT |
1.5 |
|
wellwidth |
diameters |
1.2 |

References:
Sharma, R. V.; Sharma, K. C. Physica, 89A, 213. (1977).
5.3. HayterMSA Structure
This calculates the Structure factor (the Fourier transform of the pair correlation function g(r)) for a system of charged, spheroidal objects in a dielectric medium. When combined with an appropriate form factor (such as sphere, core+shell, ellipsoid etc…), this allows for inclusion of the interparticle interference effects due to screened coulomb repulsion between charged particles. This routine only works for charged particles. If the charge is set to zero the routine will self destruct. For non-charged particles use a hard sphere potential.
The salt concentration is used to compute the ionic strength of the solution which in turn is used to compute the Debye screening length. At present there is no provision for entering the ionic strength directly nor for use of any multivalent salts. The counterions are also assumed to be monovalent.
|
Parameter name |
Units |
Default value |
|
radius |
Å |
20.8 |
|
charge |
|
19 |
|
volfraction |
|
0.2 |
|
temperature |
K |
318 |
|
salt conc |
M |
0 |
|
dielectconst |
|
71.1 |
References:
JP Hansen and JB Hayter, Molecular Physics 46, 651-656 (1982).
JB Hayter and J Penfold, Molecular Physics 42, 109-118 (1981).
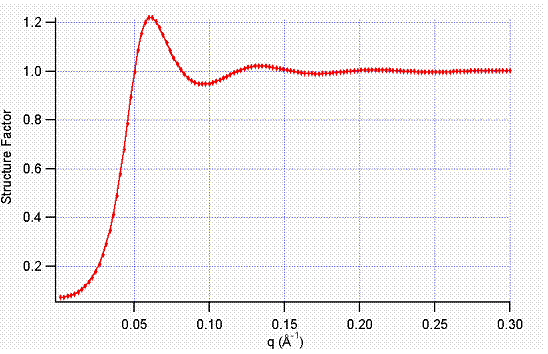
5.4. StickyHS Structure
This calculates the interparticle structure factor for a hard sphere fluid with a narrow attractive well. A perturbative solution of the Percus-Yevick closure is used. The strength of the attractive well is described in terms of "stickiness" as defined below. The returned value is a dimensionless structure factor, S(q).
The perturb (perturbation parameter), epsilon, should be held between 0.01 and 0.1. It is best to hold the perturbation parameter fixed and let the "stickiness" vary to adjust the interaction strength. The stickiness, tau, is defined in equation 21 and is a function of both the perturbation parameter and the interaction strength. Tau and epsilon are defined in terms of the hard sphere diameter (sigma = 2R), the width of the square well, delta (same units as R), and the depth of the well, uo, in units of kT. From the definition, it is clear that smaller tau mean stronger attraction.
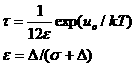
where the interaction potential is

The Percus-Yevick (PY) closure was used for this calculation, and is an adequate closure for an attractive interparticle potential. This solution has been compared to Monte Carlo simulations for a square well fluid, with good agreement.
The true particle volume fraction, f, is not equal to h, which appears in most of the reference. The two are related in equation (24) of the reference. The reference also describes the relationship between this perturbation solution and the original sticky hard sphere (or adhesive sphere) model by Baxter.
NOTES: The calculation can go haywire for certain combinations of the input parameters, producing unphysical solutions - in this case errors are reported to the command window and the S(q) is set to -1 (it will disappear on a log-log plot). Use tight bounds to keep the parameters to values that you know are physical (test them) and keep nudging them until the optimization does not hit the constraints.
|
Parameter name |
Units |
Default value |
|
radius |
Å |
20.8 |
|
perturb |
|
0.05 |
|
volfraction |
|
0.1 |
|
stickiness |
K |
0.2 |

References:
Menon, S. V. G., Manohar, C. and K. Srinivas Rao J. Chem. Phys., 95(12), 9186-9190 (1991).
Feigin, L. A, and D. I. Svergun (1987) "Structure Analysis by Small-Angle X-Ray and Neutron Scattering", Plenum Press, New York.
Guinier, A. and G. Fournet (1955) "Small-Angle Scattering of X-Rays", John Wiley and Sons, New York.
Kline, S. R. (2006) J Appl. Cryst. 39(6), 895.
Hansen, S., (1990) J. Appl. Cryst. 23, 344-346.
Henderson, S.J. (1996) Biophys. J. 70, 1618-1627
Stöckel, P., May, R., Strell, I., Cejka, Z., Hoppe, W., Heumann, H., Zillig, W. and Crespi, H. (1980) Eur. J. Biochem. 112, 411-417.
McAlister, B.C. and Grady, B.P., (1998) J. Appl. Cryst. 31, 594-599.
Porod, G. (1982) in Small Angle X-ray Scattering, editors Glatter, O. and Kratky, O., Academic Press.